函数重要模型-所长林超多元思维模型整理笔记（五）

文章目录

函数
时间函数
总结
原视频地址
自我感想

函数

“函数”是数学带给这个世界最好的礼物之一。
数学家 Jordan Ellenberg （乔丹艾伦伯格）曾经画过一张非常经典的图，他把数学分成四个区域
数学的四个区域
1号区深奥、复杂
比如庞加莱猜想、费马最后定理，黎曼假设等。
2号区深奥、简单
比如指数函数、对数函数、拉弗曲线、大数定律等。
3号区浅显、简单
比如加减乘除，开方乘方等。
4号区浅显、复杂
比如复杂定积分，这个区域充满了唬人的公式。

（个人感觉这样的区域分类没有好大意义）

对我们大多数人而言，深奥、简单的2号区里的数学是最有价值的，因为它们通常非常实用，而且简单直观。
而函数就是2号区域里面最重要的组成部分，这就是我们今天讲函数的最重要的原因。

但在日常生活中，每当我跟非理科生说起函数时，大家总是一脸茫然，就好像函数是特别高深的东西。
函数不难，它是初中数学就有的概念，你觉得它难，原因之一是教科书为了追求严谨，通常爱把简单的东西说得极其抽象。

比如初中数学教科书对函数的定义：
在一个变化过程中，有两个变量， X 与Y。如果对于 X 的每一个值， Y 都有唯一的值与它对应，那么就说 X 是自变量， Y 是 X 的函数因变量。
你说这种定义，能记住才怪。

其实函数这个东西之所以直观，就是因为它通常都能简化成图形，而图就能够直观地告诉我们一个变量和另外一个变量的关系(大脑对图形的理解远远好于数字，这点查理也说过这样的论断)。
函数就是把一个变量跟另一个变量一一对应起来的图

时间函数

在我们自己的生活中，我发现最有用的一类函数，实际上是时间函数：

横轴（自变量）：时间
纵轴（因变量）：收益、营业额、价值、能力、价格、情绪、精力等
这些变量的变化和时间之间的对应关系，就是时间函数。

时间函数之所以强大，是因为它可以给我们提供一个穿透时间、预测未来的上帝视角。

我们普通人，在生活中遇到最大的挑战就是短视，最近一段时间的境遇会极大影响我们对未来的判断。
比如，有一个人最近过得很糟糕，那么他就会倾向于认为未来同样很糟糕，但实际上，未来有可能会突然变好，也有可能是每况愈下。
如果没有时间函数作为依据，其实就没有任何评估的基础。此时如果你把历史时间函数拉出来，有可能会茅塞顿开。
★1.高特纳曲线
高特纳曲线（Hypecycle模型），可以用在生活中的很多方面。
hype cycle，该模型由著名咨询公司Gartner发布，包含Gartner对众多行业发展周期的预测与判断。
这条曲线非常经典，它的函数形态是这样：

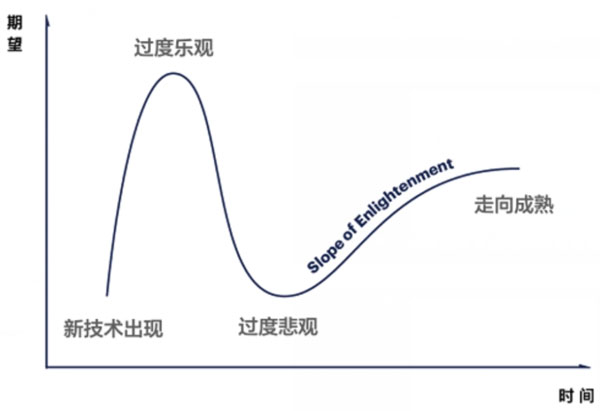
【新技术出现】→【过度乐观】→【过度悲观】→【走向成熟】
在一个新的技术出现之后，整个世界通常会过度乐观、过度兴奋，觉得这个世界马上会因此而改变。
但接下来当技术开始落地时，大家又会重新陷入到过度悲观，因为它没有发展这么快，世界并没有因此焕然一新，
所以后来大家觉得这个技术也没什么了不起，就逐渐把它淡忘了。
但在这之后，这个新技术又会慢慢地重新成长起来，在远离大众视野的地方，逐渐走向成熟。

邓宁-克鲁格效应

这条曲线的形态，也符合我们生活中很多事情的变化规律。

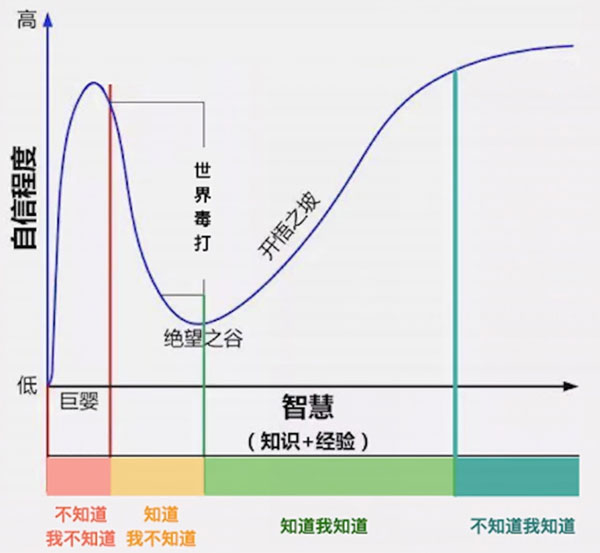
克鲁格效应

我们在年轻时，通常觉得自己无所不知，自信程度非常高；
然后随着我们逐渐长大，从中学到大学，从大学到社会，就是不断经历被社会毒打的过程。

比如中学成绩很不错，结果考上大学后跟同学一对比，跟周围的环境一对比，你就发现自己没有那么厉害，
此时自信心会跌入谷底，然后再重新慢慢攀爬起来。

当你从大学毕业又进入社会，又一次会被社会毒打，
自信心又一次跌到谷底。

当你从一个行业进入到另外一个行业时，通常也会发生这样的现象，
总是先跌落谷底，再慢慢往上攀爬，有可能再次跌入谷底，然后再往上翻盘。

我们人生遇到很多境遇，都符合这个规律——
不要高估短期能发生的变化，
不要低估长期能发生的变化。
我们通常不要高估两年内能发生的变化，但是也不要低估长达十年能发生的大变化；
不要高估坚持两个月能做的事情，但也不要低估坚持十个月能达到的成果。

产生原因
如果我们再深入一层来研究一下，为什么会有这条曲线，它是什么产生的？
实际上这条曲线是由两条完全不同的曲线构成的——人性曲线&物性曲线。

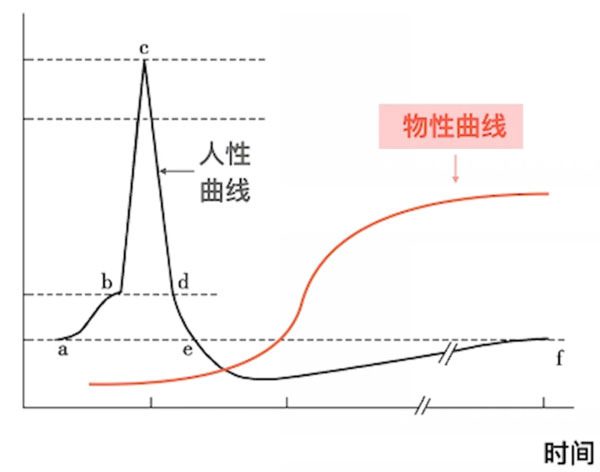
人性曲线
人性曲线是怎么来的呢？
从生物学的角度，这是细胞膜电位和时间的函数图（也是一个时间函数），它是神经科学里非常有名的一条曲线（如下图）。

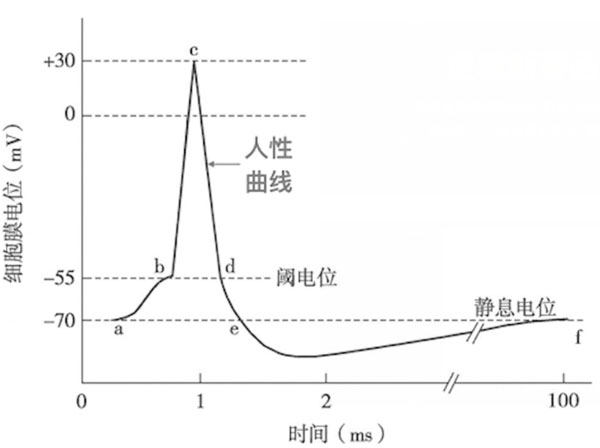
当我们受到刺激，如果刺激超过了某个阈值，整个神经电位就会飞升，一下子跳到很高的 C 点（如下图）；

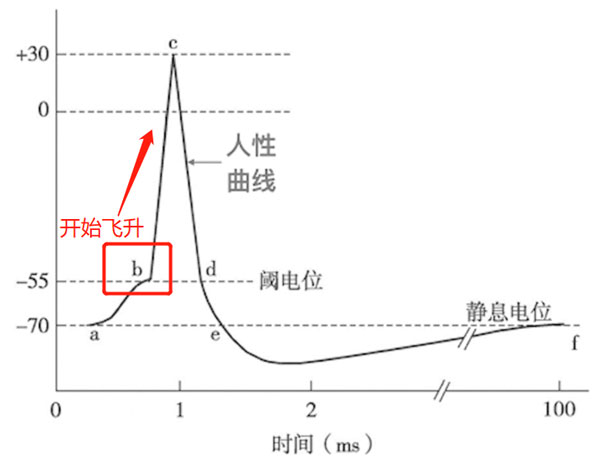
然后又从 C 点再次重重跌回来（如下图）。

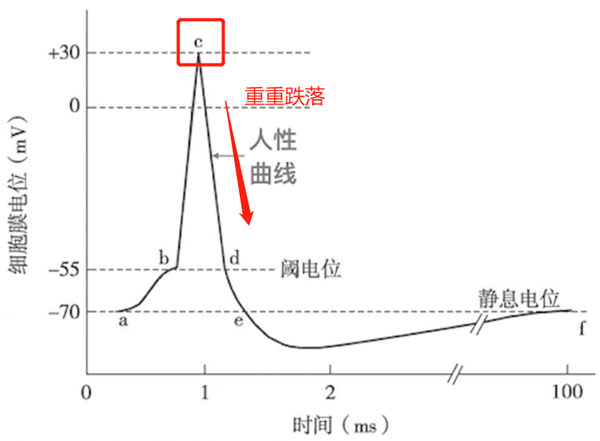
这个下跌的过程，往往会过度的下跌，然后又会重新恢复到平静，此时会达到一个相对稳定的状态——静息电位（见上图后时间轴后截）。

这是我们收到各种刺激时，细胞电位反应情况，它实际上就是人类遇到各种刺激情况下的缩影。
我们的很多反应都逃脱不了这样的反应曲线，所以我们把它叫做人性曲线。

高特纳曲线的另外一个部分——物性曲线，此处就要提到另一个非常重要的事物发展函数——逻辑斯蒂函数。

★2.逻辑斯蒂函数
逻辑斯蒂函数（Logistic Equation）是数学家 Pierre-Francois Verhulst 提出的一个非常著名的人口增长模型。
这个函数被发现可以广泛应用在生物学、医学、经济学、管理学等很多的领域，可以描述很多事情经历高速增长之后，逐渐迈向稳定的过程（如下图）。

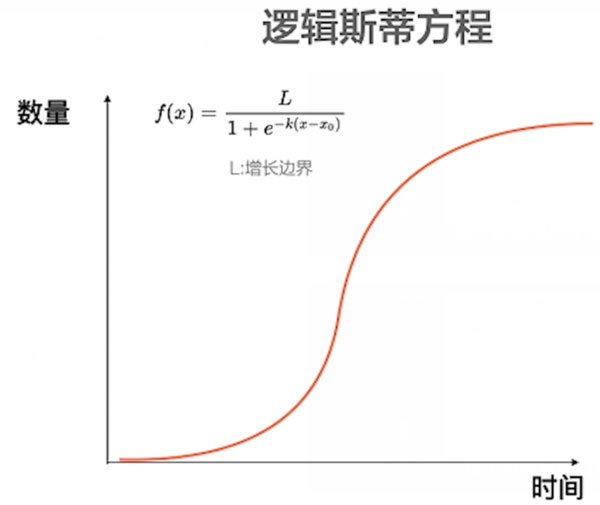
公式的分母 L 代表整个逻辑斯蒂函数的增长边界。
这个函数是一个数量-时间函数，描述随着时间增长，数量是如何变化。
可以看出来，随着时间增长，数量一开始慢慢长大；
但到了后来，突然间变得非常陡峭，因为跨过了一个拐点；
然后这个陡峭的向上曲线又遇到一个玻璃顶，然后逐渐收缓。

逻辑斯蒂曲线是一个指数级增长的力量和一个环境阻力共同构成的一条曲线。

指数级增长的力量：在一个资源丰裕的环境下，如果没有任何限制，那么不管是人口还是羊群，都会形成一个指数级增长的形态。
当指数增长到一定程度之后，就会遇到一个环境阻力线（如下图虚线）。
然后这条阻力线会把逻辑斯蒂增长挡在一个增长极限里面，这就叫玻璃顶，所以它会让蓝色增长曲线变成红色增长曲线（逻辑斯蒂增长曲线）
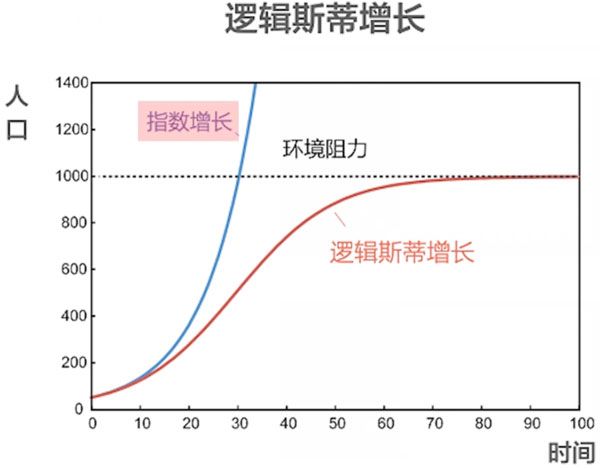
逻辑斯蒂曲线
这非常符合我们日常生活中遇到的真实情况，人类社会的发展也是如此（如下如）：

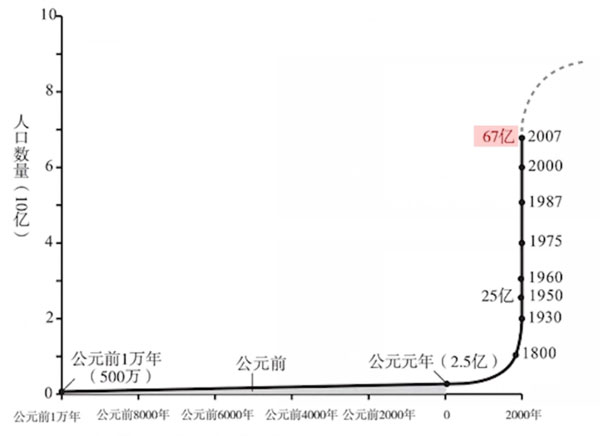
公元前 1 万年时，人口非常少；
直到公元元年，这条曲线仍然是非常平缓在进展；
元年时，全球人口才只有 2.5 亿；
之后就开始慢慢遇到拐点，短短几百年的时间里面，就从 2.5 亿→ 25 亿→ 67 亿，这个曲线变得非常陡峭。
但到了现在，我们看到很多国家，这条曲线已经出现了拐点，比如日本、德国、意大利。
很多国家的增长曲线，我们都能感受到这个逻辑斯蒂模型，它跟现实非常吻合。(25号宇宙?)
★3.倒 U 形曲线
拉弗曲线（税率-税收）

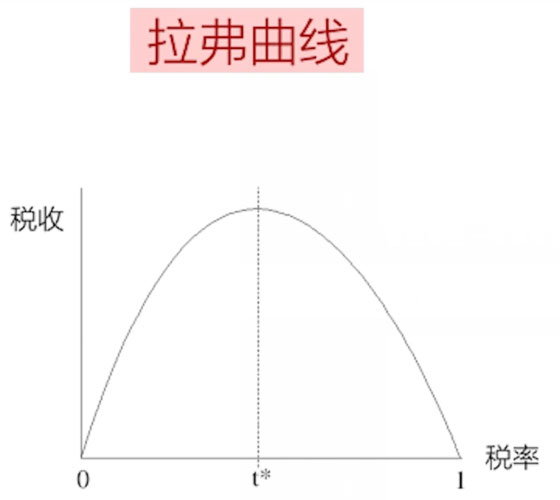
它是经济学里面有名的拉弗曲线，听起来好像很学术，实际上原理极其简单，
它是用来描述政府能够收上来的税收和税率之间的关系。
横轴：税率，税率是从 0 到1。
0：完全不收税；
1：把所有人赚的钱都收上来。
纵轴：政府能总共收上来的税收。

这条曲线的含义：在 0 和 1 之间，找到一个适当的值（税率），使得税收最高。
如果税率为0，那么收不上来任何税；
如果税率为1，那么没人愿意打工，同样收不上来任何税。
所以，税收和税率的对应关系，就是倒 U 形的曲线。

进食-愉悦度

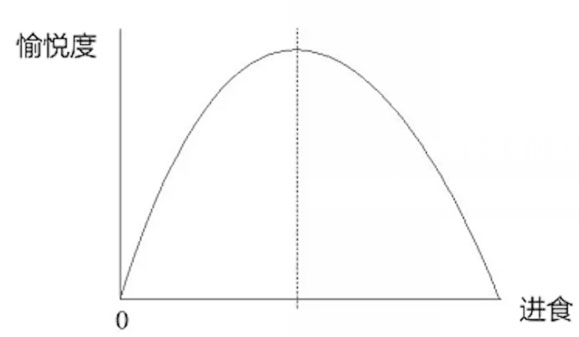
进食-愉悦度曲线
倒 U 形函数可以用在生活中很多地方，比如我们吃东西和愉悦程度之间的函数（如上图）。
如果你非常饥饿，那此时不愉悦；
随着你进食到了一定程度，愉悦度就会达到峰值。（饥饿是最好的开胃菜）
如果你继续吃，反而觉得很难受；
吃到最后，你可能把自己给撑死，愉悦度又回到0。

锻炼-健康度

锻炼和健康也是这个对应关系。
锻炼在横轴，健康在纵轴，每一个锻炼程度，跟健康度一一对应。

这就是函数，简单好用，堪称是现代人居家旅行的必备工具。

各国GDP发展图
现在我们都知道，中国和美国关系很紧张，遇到了很多阻碍，GDP时间函数会告诉你，未来中美的国力对比会走向何方。
未来中国和美国的国力对比会走向何方呢？
如果我们了解倒 U 型曲线，就可以很好地解释这个现象。
我们只需要分析过去 500 年各个大国生产力发展的函数，那么你就会发现，各种国力发展和时间的关系都是符合倒 U 形函数曲线的（如下图）。

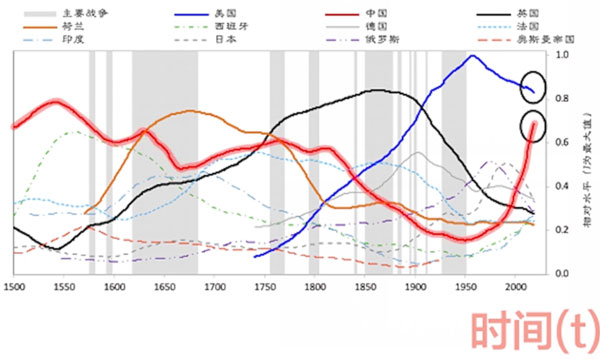
这里面一开始是中国，它是先上后下（如下图红色线），

然后荷兰崛起，也是先上后下。

英国超越荷兰，一路往下。

荷兰走完他的倒 U 型曲线路线之后，接下来英国崛起，然后美国崛起，美国起来时，英国又下去了。

再然后就是中国曲线到了谷底之后，开始慢慢沿着趋势往上走。
我们看到，中国在倒 U 型曲线的上升期，而美国在倒 U 型曲线的下降期。

所以你看两国未来的走向，就有了推测的依据，只要画出时间函数，实际上就给了我们判断事物未来走向的其中一个角度。

这个推测 100% 就准吗？
当然不是，任何一个结论都必须有多学科的视角交叉验证，但是函数视角肯定是其中一个非常重要的视角。（这是留后门嘛，说了半天的漂亮废话）
比如国家发展的倒 U 型曲线，就非常适合用来描述很多事物的发展规律。（不符合曲线的有多少？是个例还是普遍有重要参考意义，怎么感觉有点儿越来越水，没有前两期好了）

行业生命周期图

我们之前无数次讲过这样图，每一个行业都会走出刚才讲过的国家内容类型倒 U 型图，他们会经历曙光期、朝阳期、成熟期、衰退期。

生命机能发展图
人体机能发展，也符合倒 U 型发展态势（如下图）。

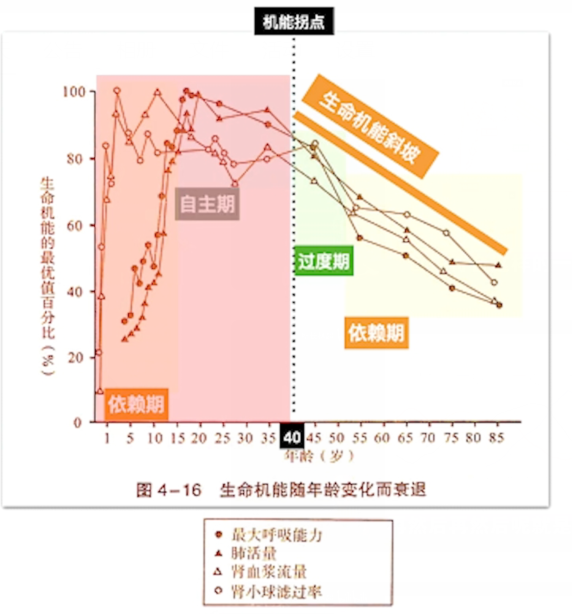
生命机体在年轻时，肺活量、肾血浆流量、肾小球功能都是往上走的；
从 5 – 15 岁，一路往上飙升，到了 20-30 岁时，就达到了人生的高峰了；
然后 35 – 40 岁时，就出现拐点，接着身体机能就一路往下。
这仿佛是很多事情从出生到衰亡的普遍规律，我们的智力发展也符合这个规律。

流体智力发展图
之前我们也讲过，人类的流体智力(Fluid Intelligence) 它跟我们的身体天赋高度相关，决定了灵活应变、学习能力这些最关键的能力。
它的发展也符合从婴儿到少年、青年、中年、老年这样的倒 U 型曲线的发展态势。

人生犯错成本图
年轻时犯错成本比较低；
到了中年犯错成本就变得非常高；
但是到了老年犯错成本又变低了，因为牵挂变少了，孩子长大了。（家族不合，孩子长大了是主因，说函数就有些牵强了）

所以我们看到很多 50 多岁的阿姨反而很想得开，开始寻找自我了，就是这个道理。

所以事物发展的倒 U 型曲线，是一个非常重要的东西，它也是普适性很强的函数。

★4.正余弦函数
普适性比倒 U 型曲线还要强的函数就是正（余）弦函数，它对应的一种函数形态就是波动（如下图）。

波动就是时间的伴侣，有很多变量的时间函数都是符合波动规律的。
比如我们的人生境遇、情绪、心跳。

人生通常在经历波峰之后就会回到波谷，波谷之后就会回到波峰；
情绪通常在兴奋之后，又会变得压抑；
股价通常在大涨之后就会向下回调。
这些都是我们无法逃避的，所以波动函数无所不在。

波动函数的启发
最近你过得不顺利，时间函数会告诉你，现在是黎明前的黑暗，还是凛冬将至。
回到开头的那个问题，假如说最近你过得很不顺利，那么接下来会怎么样呢？
通过时间函数的套用，你就可以推测出来，这种不顺利，它到底是黎明前的黑暗，还是黑夜前的黄昏。

你过得不太顺利，在时间函数中的表现是这样的，随着时间的推移，你的收益在一路往下走。

黎明前的黑暗
当你用它套在时间波动图里，你就会看到，也许它只是整体上升趋势里面的一个波谷而已，这个就叫做黎明前的黑暗（如下图）。

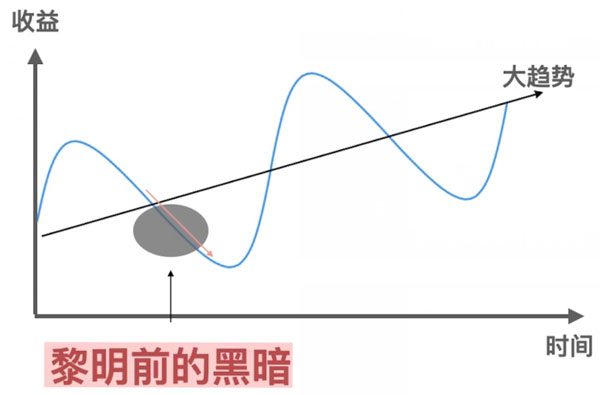
黑夜前的黄昏
它也可能是反过来的，是整体下降大趋势的一个前奏，这就是黑夜前的黄昏（如下图）。

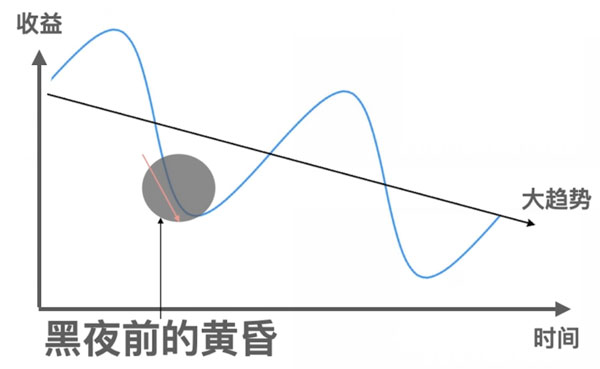
波动模型很简单的，但这里面似乎波动背后的大趋势才是关键，而读懂这个大趋势，函数解答不了。（又一个坑）

此处我们有可能要跳出函数之外去看问题，这也是我们为什么需要学习多元思维的原因。
因为要解答很多的问题，需要两个或两个以上的更多模型相互印证。

趋势的判断
如何才能判断大趋势？
通常要借助产业研究、系统论、管理学、金融学、政治学、历史学等其他知识。

比如如果你了解系统论，那你就可以通过分析一家公司的商业模型，了解这家公司的竞争力。
我自己在 2018 年的时候，就曾经通过系统论的分析，找到了一个黎明前的黑暗。

例一投资奈飞盈利
美股有一家公司叫做奈飞（Netflix），它出品过《纸牌屋》等知名电视剧。
Netflix(Nasdaq NFLX) 美国奈飞公司，简称网飞。是一家会员订阅制的流媒体播放平台
《纸牌屋》（House of Cards）由奈飞公司（Netflix）出品的政治题材电视剧，六季共73集
18 年 9 月份，这家公司的股价有过一次非常重大的下跌，
因为当时美国有好几个大的竞争对手都宣布要大力地进军流媒体行业，所以市场觉得奈飞的好日子到头了。
但是当时我判断这家公司的竞争力非常强，竞争对手并不能够轻易地复制它的成功。

为什么我觉得它有很好的商业模式呢？
使用系统论的分析方法，详细讲解在学科02：系统论重要模型，这里直接说结论：
我当时发现，奈飞处于一个非常经典的系统论良性循环里面，马太效应非常明显。

简单来说就是奈飞通过砸大钱，自己制作电影、电视剧的方式，提供了独特的竞争力，独家自研内容越多，会员增长就越快；
而会员增长越好，口碑传播就越好。会员增长本身又可以给奈飞带来最直接的会员收入。
因为奈飞的收入模式是必须付费才能看（跟国内的各大视频网站完全不一样），所以只要他的会员一增加，它的收入就会不断的增长；

而收入不断增长之后，自研内容的投入也会不断增加，所以他的自研内容就会越做越强，进一步吸引更多的用户成为它的会员。
然后他的自研内容又形成了自己的小闭环。

作为市场上投资新剧最大的金主，所有的导演和演员都会优先考虑和奈飞合作，而这又使他更容易拍出好剧。
这三个循环相互咬合，让这家公司不断地处于一个自增强的良性循环里面，所以我觉得这家公司的未来一定可以在竞争中获胜。

所以当时在奈飞股价下跌了 30% 的时候，我做了一些投资，事后证明这笔投资在两年时间里面，给我带来了超过 100% 的回报。

例二错过教育行业
我在 2013 年研究过，要不要进入在线教育这个行业，因为我的全家人几乎都是老师，我的父亲、母亲、伯父都是当老师，所以我对教育行业还是很有好感的。

当时刚好我的上一家公司卖掉，手头有一点点资金，所以我就非常深入地研究了要不要进入在线教育这个行业，但在尝试了半年之后，我就放弃了。
因为 13 年这个行业太难了，根本没有成立的商业模式，即我刚好经历了这个行业的一个低谷，后来我就放弃了。

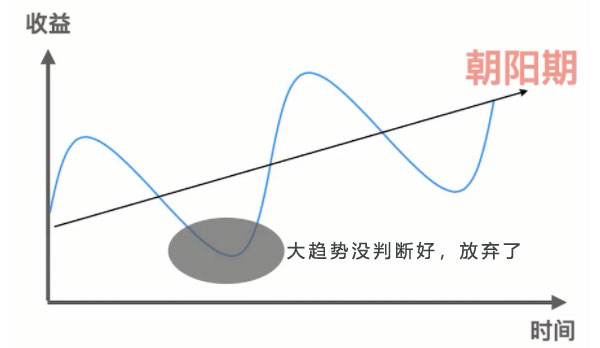
错过教育行业
而就在我放弃之后的几个月，整个行业里面，有很多公司开始纷纷宣布获得融资，投资机构纷纷进场。
之后的三年，被称为中国在线教育的元年，很多创业公司在那段时间都发展得非常好。
这就是典型的在朝阳期开启之前，刚好我进去时经历了低谷，然后我就放弃了。

当时我的最大问题就是，我只盯着自己的一亩三分地，而没有去跳到更高维度，看整个行业发展的大趋势，即我没有画出来这个行业发展的函数曲线图。

如果我可以适当做一些行业的发展历史的分析，也许就能够发现，整个行业的发展大趋势其实非常明显，只是我自己刚好遇到了一个小低谷而已。
所以如果我们自己正处于一个朝阳的赛道，那么一定要记住，不要因为眼前遇到一点小挫折，就放弃这个赛道的大机遇——一叶障目，不见泰山。

例三 APP创业失败
在 2015 年，我当时拿到一笔千万级融资，创业做了一个在线交易的APP。

当时的大环境是什么样子呢？
做手机 APP 这件事情已经越来越不吃香了。
业内的话，叫做移动互联网的流量红利已经逐渐消失，就是获取每一个互联网用户的成本越来越高了。

但是当时刚好是一个投资的小阳春、小高潮。
很多投资人开始拿钱涌进来，想要去投新的移动互联网项目，此时阴差阳错我拿到了钱，可以说刚好碰上了一个回光返照。

所以在 2015-2018 年的三年内，尽管我拿到了钱，微观层面上趋势不错，但是整个行业大的趋势，却是一路往下走，
所以我越做越困难，最后烧光了 2 千万，什么也没做成。

这是另外一个典型的例子。就在一个行业整体衰退的大形势下，你刚好遇到了一些好机会，然后你就冲进去了，
于是你把自己给锁死在这件事情上面，不得不陪着整条赛道不断地往下坠落。

所以这给我们另外一个启发，就是
不要因为短期看起来光鲜亮丽，就忽略了整体下降的大趋势。
不要因为短期看起来光鲜亮丽的微观形式，就忽略了你现在所处的宏观大环境，或者大行业整体下降的大趋势。

这方面，正面的例子 UP主小艾大叔，

他很明智地从一个整体下降的大行业——房地产业，跳到了一个整体上升的行业——内容行业。
尽管他之前在房地产行业做得已经很成功了，但他还是义无反顾地迁移到了新兴行业从零开始，我觉得（？）这个就是明智的选择。

回到函数的知识里面，波动函数真的是无处不在。
瑞达利欧大小周期曲线

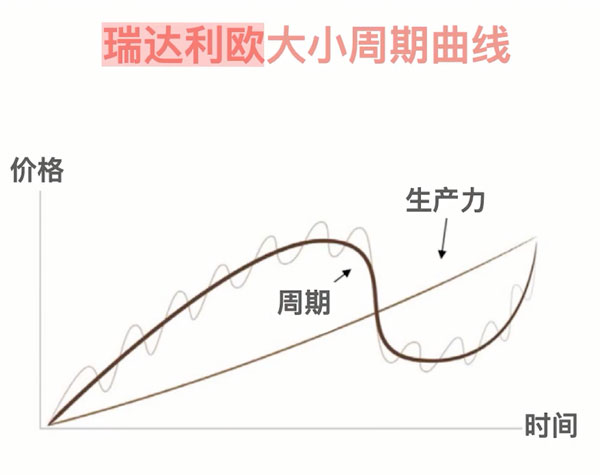
所以，瑞·达利欧曾经画过一个产业发展的大小周期曲线图。
瑞·达利欧（Ray Dalio），桥水基金的创始人。著《原则》
他认为，这个世界的发展就是很简单的由三条曲线构成的，
第一条曲线是小周期，小周期会围绕一个大周期去波动，而大周期又会围绕一个更大的、不断成长的生产力发展函数波动。
那么这三条曲线叠加在一起，就构成了人类经济活动的整个时间函数。

所以我们很多时候人生经历的，只是这个大周期里的某个小周期里非常小的片段。（通俗来点讲就是活在什么时代就是什么时代的人）
如果我们可以跳出来看到整个大环境，那么的确更不容易受到很短期趋势的蒙蔽。

★5.指数函数
指数函数是一个增长奇迹函数。

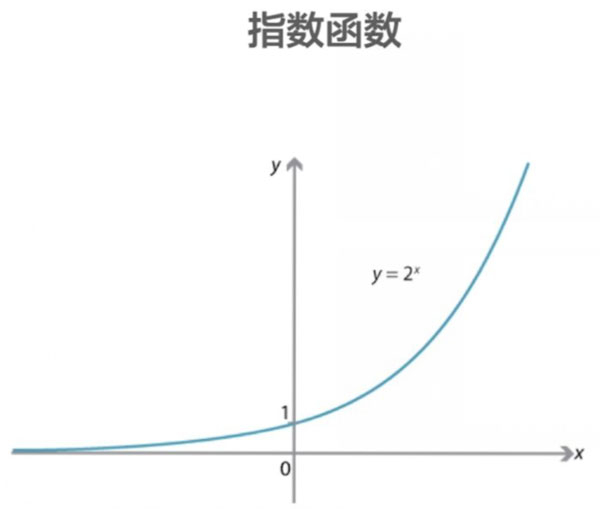
相关名词：复利效应、爆发式增长、裂变式营销
相关场景：各种丧尸片中描述的场景（病毒的传播、丧尸数量的增长）

优势
通常只要是跟指数函数相关的东西，产生的效果都是非常戏剧性的。

比如细胞的裂变、想法的传播、病毒的传染、传销组织的壮大，都是这样一个裂变过程：
模式上都是一传二、二传四、四传八、八传十六，表面上看传了 4 级，也就只是从 1 变成了 16 而已，这时候看起来并没有多少，
但你想想如果能够连续传 40 级，这个数字就会变成 1 千亿，这就是指数级裂变的强大威力。

一旦这个系统运转起来，开始尽管非常缓慢，但是后来会突然爆发，让所有人都惊掉下巴。
劣势
同时从这个模型里，我们能看到指数级增长的脆弱性，如果早期其中的某个关键链路断掉，则整个增长的模型就会崩塌。

举个最极端的例子：
如果有人给你一个鸡蛋，然后他说：
“这个鸡蛋只要孵出小鸡，然后小鸡不断地在蛋生鸡，鸡生蛋，未来你就可能成为亿万富翁。”
这时候你听了会非常高兴。
结果没有半天这个鸡蛋打碎了，瞬间损失了一个亿。
这就是指数级增长的脆弱性。

应用
技术进步复利效应
其实很多事情的发展都符合指数函数的特征。
拿技术进步来举例，比如突然出现一项新技术，开始时没人看好，它只能在小圈子里面更新迭代不断优化。
但有一天当它开始成熟出圈时，就会发现几乎所有的领域都跟它产生关系，然后一传十、十传百飞速传播。

例一互联网+
互联网当年的发展就是这样，当它破圈时，几乎任何东西都可以与互联网产生关系，转换成为互联网+ 。

例二电力时代
一旦电相关技术发展成熟，跨过了拐点，人们一下子就发现几乎万事万物都能用上电。
汽车、做饭、洗衣服、工厂等都会用上电，于是用电的规模就会爆发式的增长。

例三通讯工具——微信的传播
当初每个知道微信的人，肯定会让自己常联系的人也用上微信，这样子才能够体现微信它作为通讯工具的本质价值。
人传人最可怕，所以当年微信仅用了 10 个月的时间，就几乎传遍了大江南北。

传闻、流言、八卦、潮流时尚同理，只要有人传人的特性，很多都具有指数增长效应。

迷惑性
指数函数最特别的地方是它在早期发展的时候极其具有迷惑性。
比如新冠疫情，早期发展时，全世界都觉得这个事情不是个事儿，因为一开始看它的发展极其缓慢，然后突然间就快得让人难以置信。

究其原因是我们人类大脑无法从直觉上理解指数函数的。
因为在原始人类的生存环境里面，我们很难遇到指数级增长的东西，这就导致很多普通人的大脑根本没有进化出能够理解指数函数的本能。
那么这也就导致我们非常容易忽略身边的这一类事物的存在。
这一点跟我们前面讲过的倒 U 形函数和波动函数不同，这两个类函数都在人类直觉覆盖的范围区域内，所以我们很容易就注意到它们的存在。

指数函数非常不同，即使是专家，有时也会无意间忽略它们。
当时在 2020 年 3 月份新冠疫情全球确诊病例是4 万例，放在全球人口里它是非常小的数据。
如果看到这个数字增长的曲线，2 月 19 号到 3 月 1 号，整个几乎是平的，你会觉得这个疫情没有什么了不起（如下图）。
指数函数

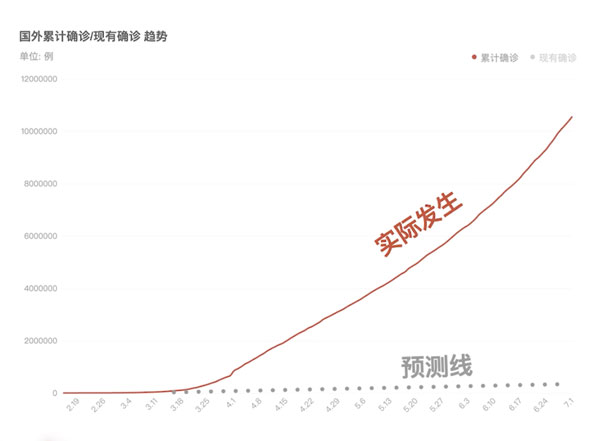
当时很多欧美国家在这个阶段几乎都是吃瓜心态，觉得新冠疫情就是中国人自己的问题。
很多欧美国家对于自己国家的新冠疫情的预测，像上图那条虚线那样。
因为仅凭直觉，他们觉得自己的国家里面这么少的案例，是不会发生任何影响的。（此处应该从病毒传播学来解释会更客观）

但实际的情况大家都知道了，是如上图红线那样，跨过了一开始的拐点，它就开始飞速往上拐，而且中间并没有发生任何特别的情况，
这个病毒当时并没有变异，也没有增加它的传播概率，它只是一直维持自己的传播特性。
只不过这个传播特性在数学上刚好吻合了指数增长的特点，所以会出现一个所谓的拐点。

所谓突然爆发，通常并不是突然爆发，而是它一直在爆发，只是一开始你没注意到。（防微杜渐）
这就是指数函数的一个非常重要的特征。
所以知道和理解指数函数这种现象，对于我们来说非常重要。

假设你有机会进入到一个指数级增长的行业，或者有机会在自己身上去引发某些指数级的变化，那么你就要打起十二分精神来，
因为你只要赶上一次指数级增长，你的人生就可能会彻底改变。

★6.对数函数
对数函数是指数函数的反函数

对数函数
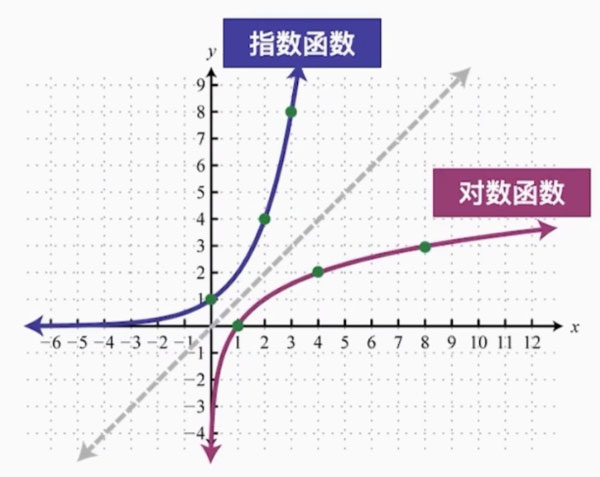
反函数的意思就是这两个函数，刚好形态上是完全反过来的。

指数、对数函数特点
指数函数特征：先慢后快，突然爆发。
那把它反过来是什么呢？
对数函数特质：先快后慢，出道即巅峰.
一出来时它就非常厉害，但到了后面，就慢慢没有任何变化。

玻璃顶效应
那么为什么会出现对数函数这样的函数形态？
因为很多的事物它会遇到一个东西——玻璃顶效应。

例一：时间约束——送外卖
比如你去送外卖，你一天都干活，不吃饭不睡觉，那你总共也就只有 24 小时的工作时间，不可能因为你非常努力，你每天就能拥有100 个小时，
那么 24 个小时就是你的玻璃顶，它不可能无限增长，不可能被突破，这就是时间约束。

例二：空间约束——共享单车
比如共享单车项目会受到空间约束，一个城市所有的公共地段、区域能够摆放共享单车的数量是有限的，所以共享单车的数量是不可能无限增长的。
尽管一开始时，你可以不断迅猛投放很多辆车，看似没有天花板，但是铺到一定程度，就一定会遇到一个玻璃顶，这就是空间约束。

例三：青春约束——嫩模职业
比如嫩模行业有青春约束，卖的就是自己的青春，就是我们常说的吃青春饭，即这个行业最值钱时，可能就是刚刚出道时，
而且随着年龄增大，她的价值就会不断下跌，这就是青春约束。

例四：内在价值约束——靠广告维持销量的产品
比如有个产品很会营销，一开始铺天盖地的打广告，但结果发现一打广告销量就上得非常快，但很快只要停下来不打广告，销量就马上停止增长，遇到玻璃顶。
这意味着这个产品本身，其实很可能没有任何内在价值，它不会传口碑，所以它的曲线就变成了一个对数函数曲线。

★7.凹形/凸形幂函数
下图是一个时间-规模的函数，中间有一条对称线（y=x）。
所谓的凹函数，你可以简单地理解为，把这条对称线往下按压，形成了一种函数形态。
所谓的凸函数，跟它相反，把这条对称线往上推，形成了一种函数形态。
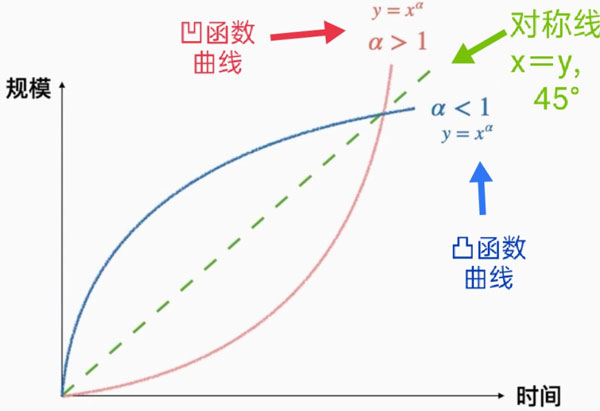
凹形/凸形幂函数
凹形幂函数的公式 y=ax, a>1 (比如y=x2 , y=x125 )

价值
凹形幂函数有什么样的特点，为什么我们需要讲它呢？
因为它实际上代表了我们生活里面一种非常强大的，可以长期增长，而且不会遇到玻璃顶的函数形态。

著名的物理学家杰弗里·韦斯特《规模》里写道，通过分析研究后发现，头部国家和头部城市的发展形态就非常符合凹形幂函数，它们都是时间的朋友。
随着时间的推移，它们的增长不仅不会停下来，而且会变得越来越健康。
这种国家和城市一开始的发展都不会特别抢眼，但是有一天就会开始突破对称中线，而且一旦突破后，就会越走越远，越升越高。

所以了解了凹形幂函数的意义，就知道这个世界上是存在一些事物，或者存在一些职业，真的是没有天花板的。

四种函数的对比
逻辑斯蒂函数、对数函数、凸形幂函数和凹形幂函数，现在我们把这四个函数放在同一个坐标系里对比一下。

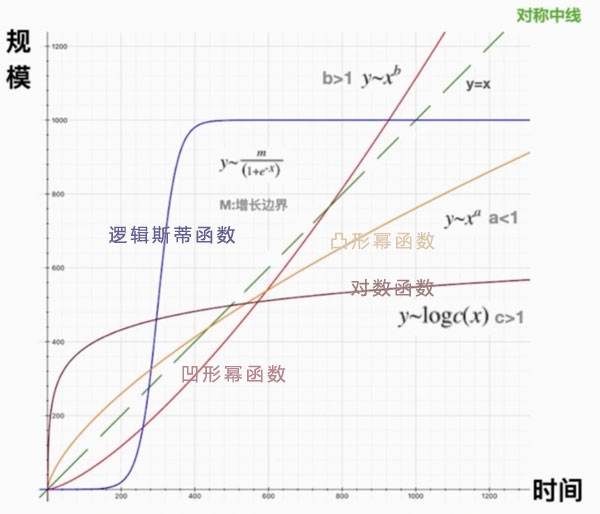
对国家/城市的启发
头部国家和城市的发展曲线都是符合红色线的形态，他们通常都能够不断发展，几乎没有尽头头。

而一旦变成了腰部的国家和腰部城市，那么就会退到符合黄色线的形态。这种形态，虽然也能不断发展，但是增速可能会越来越慢。

所以这么看来，头部的国家和非头部的国家之间的发展函数是有着本质的差别，一种是凸形幂函数，一种是凹形幂函数。
而这两种函数随着时间的推移，他们的发展距离会不断拉大。

一旦理解了这一点，大家就能够理解为什么美国现在要拼命地压制中国，不要让中国成为世界 GDP 第一（世界头号强国）
是因为一旦中国成为世界头号强国，中国就有可能从原来的平缓凸形幂函数曲线，直接跃升到向上昂扬的凹形幂函数曲线，而彻底走上完全不同的道路。
一旦美国变成老二，就可能从原来自己一直享受的增长红利切换到一个距离越来越大的另外一种增长模式里，所以这是他非常忌惮的事情。

那除了国家大事，我们再来看一下这四类函数，对于普通年轻人，其实也有很大的启发。
对年轻人的启发
我们的人生职业可以分成四种类型——
指数函数型职业，对数函数型职业，凸型幂函数职业和凹型幂函数职业，它们各是什么东西呢？

1.指数函数型职业（爆发型职业）

逻辑斯蒂函数，对应指数函数型职业——爆发型

比如那些需要追风口型的创业者、明星、网红，他们通常都是一夜爆红，这就非常符合指数型函数的增长形态。
这种函数通常在爆发到一定程度之后，都会遇到玻璃顶。
通常为了在短期内获得较好的爆发性增长，他们必须给自己设定一个非常清晰的边界，比如
专门针对腐女市场的男星
专门针对二次元人群的游戏创业者
但是后面想要破圈到大众市场，就可能要等待很多年，甚至最终都没法成功，这是这类函数的一个特征。
而这类函数通常一开始时需要像指数函数一样，蛰伏很长时间，然后才会遇到拐点。

2.对数函数型职业（速成型职业）

对数函数，对应速成型职业——出道即巅峰

这类职业很多，因为它们就是通常所谓的宽门。只要你符合某些条件，就很容易入行，而一入行就可以迅速兑现回报。
比如嫩模、外卖员、保安、骗子、职业赌徒、游走在灰色地带的捞女，
都属于出道即巅峰，很快就能挣到钱，但是不久就遇到玻璃顶的行业，如果要突破玻璃顶，通常需要经历一次彻底的转型。

3.凸型幂函数职业（专家型职业）

专家型职业，对应凸型幂函数——时间的朋友
只不过通常随着时间推移，它们的增长会逐渐放缓。
比如有医生、律师、工程师、教师等其他领域的专家。

当然类似医生和律师这样的职业，真实的薪酬增长曲线并不完全符合凸型幂函数曲线，
因为它们都是不连续跃升的，并不像函数连续增长，所以函数曲线只是一个抽象的概括。
比如医生职业，从主治医师升迁到副主任医师，再升迁到主任医师这个过程中，每一级都会有大幅增长的新机会和收入。

4.凹型幂函数职业（探索型职业）

探索型职业，对应凹型幂函数职业
这种职业没有天花板，所谓的探索性，即它通常需要去探索一些人类未知和知识的边界。
这类职业通常没有玻璃顶，随着时间的推移，如果能够熬过最开始的阶段，那么到了后面，理论上他们职业生涯发展，就跟他们取得的突破成正比。

比如科学家、学者、艺术家、发明家或者一些价值投资人（不是投机者，而是真正意义上的投资人）
因为他们的工作是探索边界，所以理论上讲，随着人类文明的发展，他们玩的是一个无限增长的游戏。

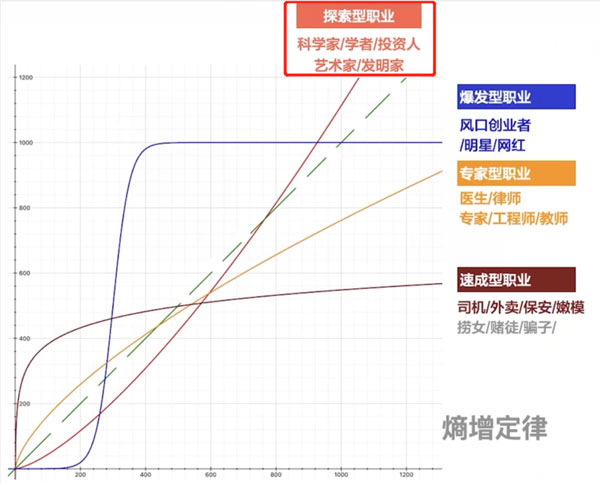
熵增定律
我们如果更深入一层会发现，这里面还有一股无处不在的向下的力量，这股力量会让这些曲线全部都面临一个向下的引力，就是熵增定律。